Er det det mer CO2 i atmosfæren som fører til global oppvarming, eller er det mer global oppvarming som fører til mer CO2?  Denne undersøkelsen viser at det er global oppvarming som fører til mer CO2.

CO2 og global oppvarming

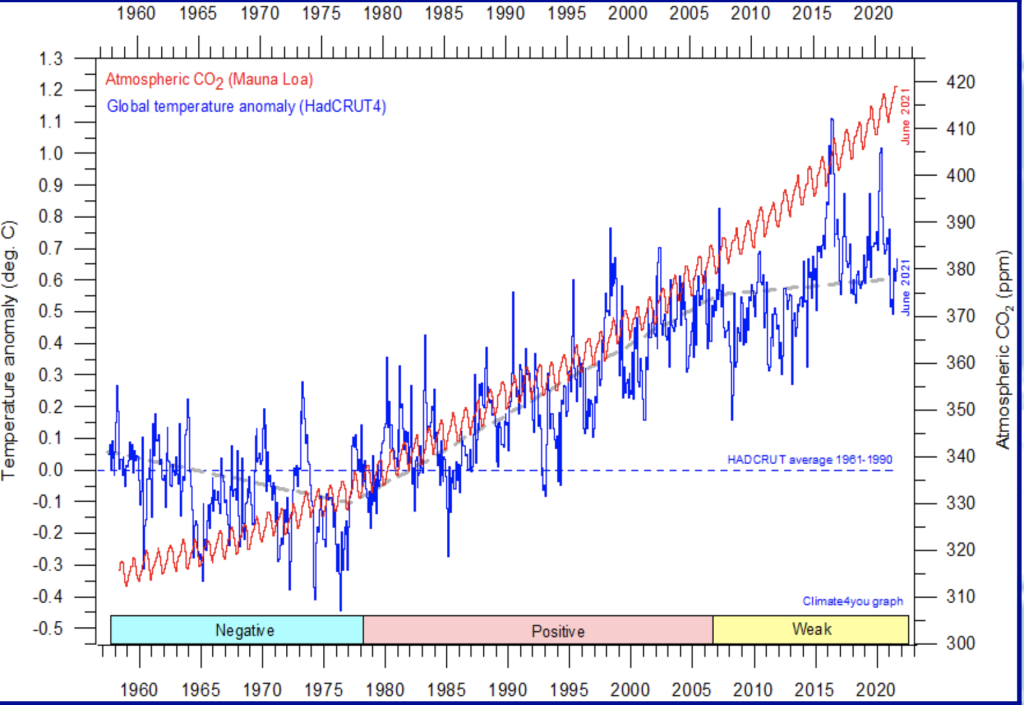
Figur 1. Utvikling av global temperatur og CO2 (per måned) fr 1950 til 2020 (Ole Humlum, Climate4you)

Denne figuren viser utvikling av global midlere temperatur (GMT) og CO2 fra 1950 til 2022. Vi ser her at GMT og CO2 har negativ korrelasjon fra 1950 til 1978, positiv korrelasjon fra 1978 til 2006 og svar korrelasjon fra 2006 til 2022. Vi ser her at GMT og CO2 er korrelerte i 28 år innenfor en samlet periode på 72 år. Det viset der er ingen direkte sammenheng mellom GMT og CO2

Når to dataserier følger hverandre, forteller dette bare at dere er en statistisk sammenheng. Dette er et godt utgangspunkt for en videre analyse. Samtidig vet vi ennå ikke hva som er årsak og virkning, eller om dette har vært en tilfeldig sammenheng. Spørsmålet er da: Er det det CO2 som fører til global oppvarming, eller er det global oppvarming som fører til mer CO2, eller var der en tilfeldig sammenheng mellom CO2 og global oppvarming i perioden 1980 til 2000? Dette ser vi ved å beregne data seriens signatur. Dataseriers signatur finner en ved å beregne frekvensspekteret.

Bakgrunn

Muligheten for at menneskeskapte utslipp av karbondioksid (CO2) kan samle seg opp i atmosfæren, vakte først alvorlig oppmerksomhet på 1930-tallet. I 1958 begynte Charles Keeling å overvåke konsentrasjon av CO2 i atmosfæren med en ny målemetode. Keeling fant at der variasjoner i CO2 som kom fra bl.a. fotosyntesen og fra urbane områder. I håpet om å finne et stabilt bakgrunnsnivå, startet Keeling målinger på fjellet Mauna Loa, Hawaii. Så viste det seg, at konsentrasjonen av CO2 ikke hadde et stabilt bakgrunnsnivå. Bakgrunnsnivået for konsentrasjon av CO2, vokste over tid. Det bekreftet mistanken om at CO2 akkumuleres i atmosfæren. Akkumulering av CO2 i atmosfæren, satte så spørsmål om effekten på havets karbonsystem.

CO2 og klima

«Den lille istiden varte fra 1200-tallet, med vekslende kalde og varme perioder, fram til ca. 1850 og en kald periode fram til 1890. Vi fikk så en varmere periode med oppvarming fra ca 1920 til 1940-årene. Fra 1940-årene til 1960-årene fikk vi en gradvis kaldere klimaperiode. Den kalde perioden varte i 1960-årene og 1970-årene. Fra 1980 og framover til år 2000 fikk vi en på nytt en varmere klima-periode, som har stabilisert seg framover mot 2020. (Se ClimateClock). I perioden 1980 og framover mot 2000 var der en direkte sammenheng mellom i global oppvarming og veksten i bakgrunn nivået for CO2. Veksten i CO2 ble forklart med menneskeskapt utslipp av klimagasser. Global oppvarming ble forklart med mer CO2 i atmosfæren. I 1960-årene begynte en å utvikle klimamodeller for å studere “drivhus-effekten”, sammenhengen mellom CO2 i atmosfæren, og global oppvarming. Fra 1980-årene og framover mot år 2000 så en at der var en direkte sammenheng mellom global oppvarming og CO2-vekst i atmosfæren. Modellene kunne nå bekrefte sammenheng mellom CO2 og global oppvarming. Dette ble tolket som en bekreftelse på “drivhus-effekten”.

CO2-vekstens signatur

Beregning av signatur, er en standard analysemetode i naturvitenskapen. Metoden benyttes til å identifisere gasser, materialer, mønster-gjenkjenning, stemmegjenkjenning osv. Alle dataserier har en signatur. Et “fingeravtrykk”, i form av et frekvensspekteret, som forteller noe om kilden til endringene i dataserier.

Dersom signaturen har stasjonære periodiske endringer, må periodene komme fra en kilde med stasjonære periodiske endringer. Eksempler på stasjonære periodiske endringer er Lunar-drevet perioder (månen, tidevannet) og solar-drevet perioder (stråling fra solen). Signaturen forteller oss om variasjonene er tilfeldige eller forutsigbare, soldrevet eller måne-drevet variasjoner. Solar-lunar perioder i data seriens signatur kan også være en tilfeldighet. Dette kontrolleres ved å sammenlikne periodenes fase, eller tidspunktet for når periodene har maksimum eller minimum. Periodenes frase, tidspunkt for maksimum eller minimum, finner en ved å benytte Wavelet spektrum analyse.

Keeling sin CO2 data serie, fra 1959 til 2020, dekker en periode på bare 60 år. Vi kan identifisere periodiske endringer opp til (2020-1960)/2= 60 år. Det betyr at vi trenger lengre data serier for å identifisere lengre periodiske endringer. 

Globalt bakgrunnsnivå for CO2 fra 1959 TIL 2020

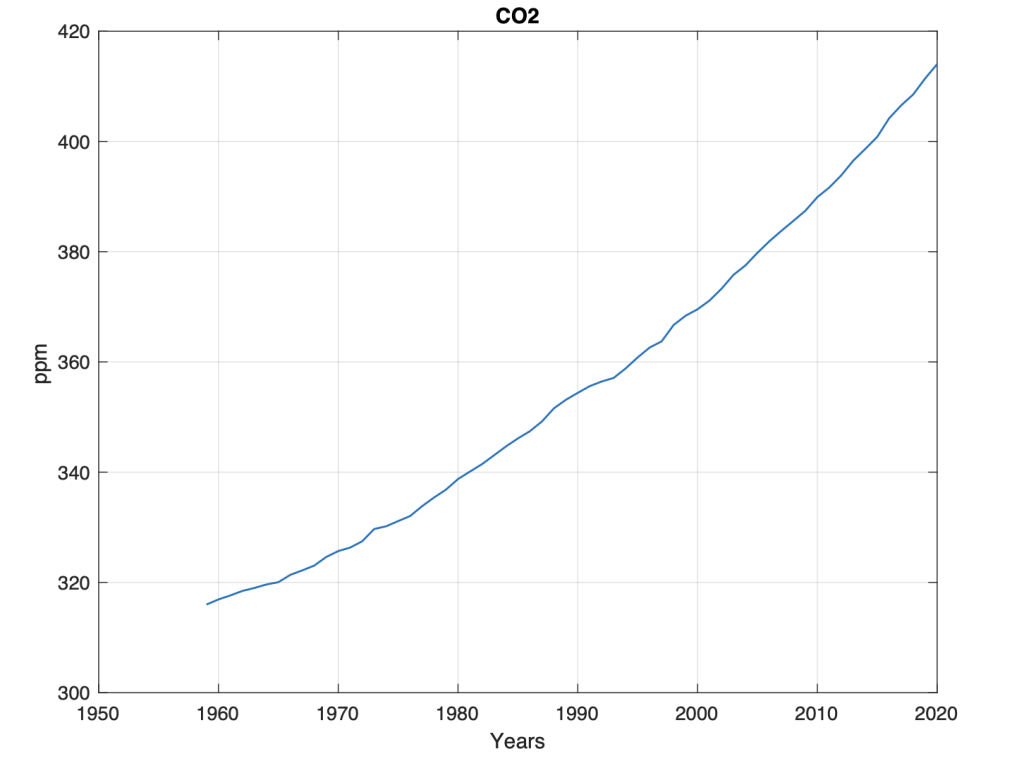
Figur 2. Mauna Loa, C02 bakgrunn nivå (ppm) for perioden t = 1959-2020

Figur 2 viser utviklingen av midlere bakgrunn nivå (ppm) for CO2 perioden 1959 til 2020, målt ved Mauna Lua, Hawaii. Det framgår av Figur 2 at bakgrunnsnivået for CO2, tilsynelatende har en eksponentiell vekst. 

Kommentar

Vi ser av figur 2 at CO2 har en tilnærmet eksponentiell vekst. Spørsmålet er hva det kan være hva som forårsaker denne veksten. En eksponentiell CO2 vekst blir forklart med at utslipp av CO2 fra fossilt brennstoff, som akkumuleres over tid i atmosfæren. En annen forklaring, er at bakgrunnsnivået for CO2 har ingen naturlig stabil tilstand. Atmosfæren er bare et mellomlager av CO2, i temperatur-drevet flyt, mellom økosystemer på land og akkumulert CO2 i havet.

CO2 vekst

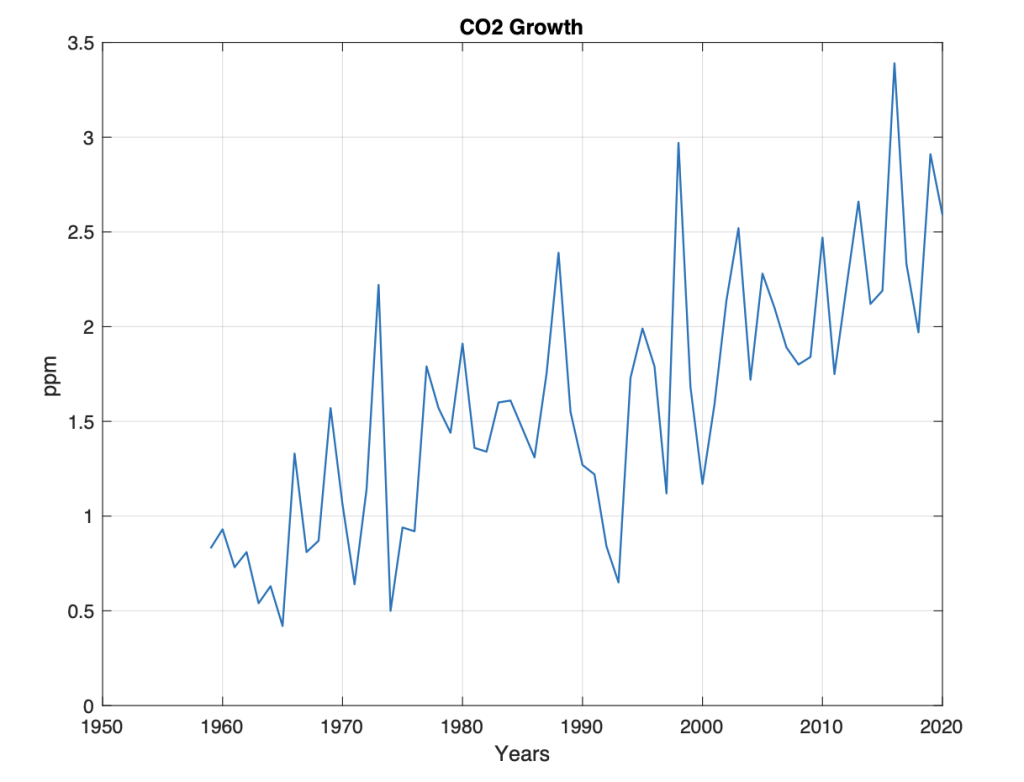
Figur 3. Årlig bakgrunn vekst i CO2 (Mauna Loa) fra årene t=1959…2020.

Figur 3 viser årlig vekst (dCO2(t) = CO2(t)-CO2(t-1)) i CO2 konsentrasjon (Mauna Loa) for perioden t=1959-2020. Her ser vi veksten i CO2 er ikke konstant. Der er store fluktuasjoner CO2 vekst for hvert år. Samtidig ser vi at veksten øker fra den kalde klima-perioden på 1960-tallet, og framover mot den varme klima-perioden fra 2010. hvordan bakgrunns-nivået for CO2 øker hvert år. Det er altså en sammenheng mellom CO2 vekst og global oppvarming. Kilden til CO2 vekst, finner vi ved å beregne signaturen til data serien.

CO2-vekstens wavelet spekter

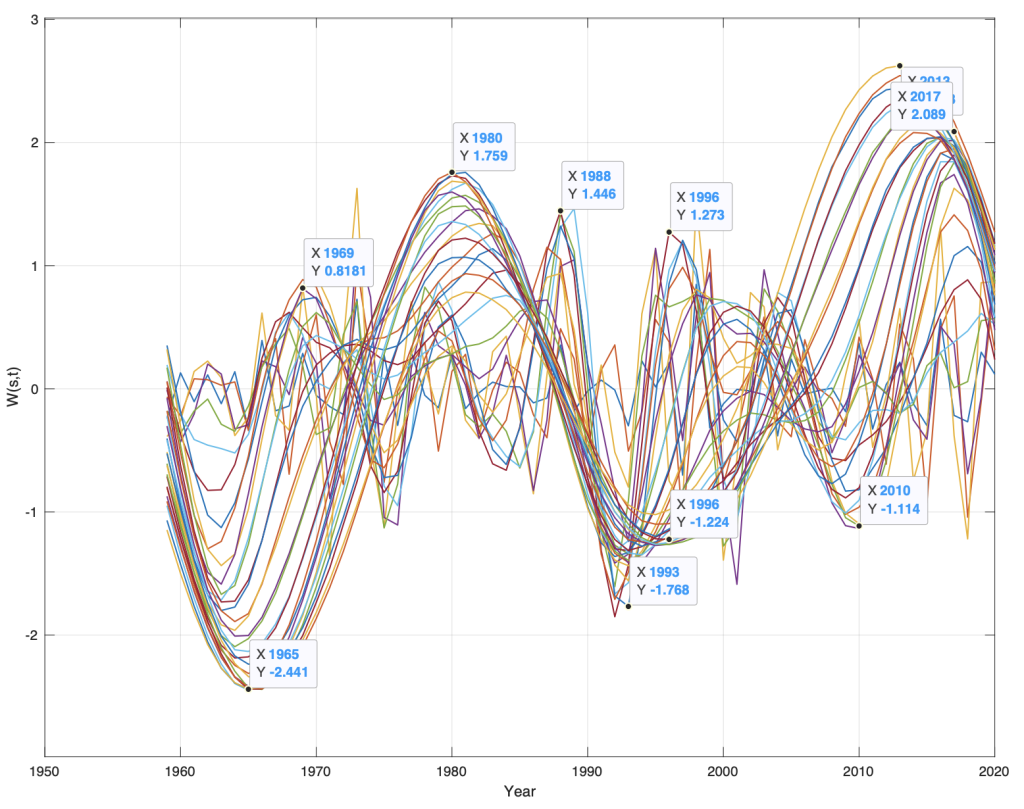
Figur 4. Wavelet spekter, W(s, t), for årlig bakgrunn vekst i CO2 (Mauna Loa) fra årene t=1959…2020.

Et wavelet-spekter er basert på en korrelasjon mellom en data serie og en klokkeformet wavelet puls (s(t)) som forflytte langs dataseriens tidsakse (t=første…siste). En får da en maksimal korrelasjon (stor tallverdi) der en har samsvar mellom wavelet pulsen og periodiske endringer i data-serien. Ved å endre pulsbredden, kan en identifisere alle periodiske endringene i dataserien. Figur 4 viser wavelet spekteret for CO2 vekst (Figur 3). Spekteret har minimum rundt den kalde perioden ved året 1965.

Wavelet spekteret W(s, t) er beregnet for CO2-vekst, dCO3(t). Den lange perioden i wavelet spekteret på Figur 4 har min/maks for årene: W(s=min/max/0, t) = [(-1.64, 1965), (-0.0, 1973), (1.8, 1980), (+0.0, 1988), (-1.2. 1995), (-0.0, 2004), (2.5, 2013)] i avstander på [8, 7, 8, 7, 9, 9] år, en midlere avstand på 8 år. Hele perioden omslutter en periode på 4*8=64 år. Wavelet spekteret har samtidig korrelasjoner for en periode med: W(s=max, t) = [(0.8, 1969), (0.8, 1979), (1.5, 1968), (1.2, 1997), (0.8, 2005)], i en midlere avstand på [10, 9, 8, 8] år, og en midlere periode på 8.75 år. Dette viser at veksten i globalt bakgrunnsnivå for CO2 ikke er sammensatt av tilfeldige endringer. Veksten i CO2 fra 1959 til 2020, har altså stasjonære periodiske endringer på ca. 9 og 64 år.

Stasjonære perioder i CO2-vekst

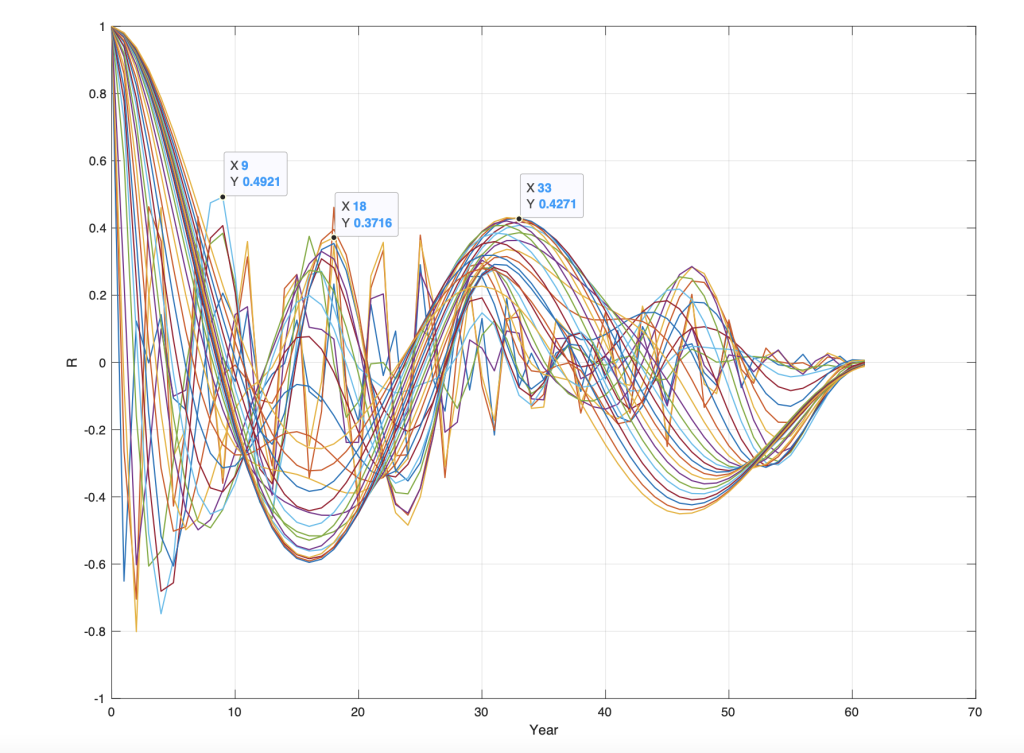
Figur 5. Autokorrelasjon av wavelet spekter WR(s), m) for årlig bakgrunn vekst i dCO2 (Mauna Loa) for s=1…60 og m=1..60.

Autokorrelasjon av et wavelet spekter beregner korrelasjonen til alle mulige periodiske endringer i wavelet spekteret. Maksimum-verdier i autokorrelasjon funksjonen (Figur 4), viser korrelasjonen til stasjonære periodiske endringer i wavelet spekteret. Altså. Først sorterer vi ut alle periodiske endringer til wavelet spekteret. Deretter finner vi periodetiden til alle stasjonære perioder i wavelet spekteret.

Stasjonære dCO2-perioder, S((t), T(), F(t)), i wavelet spekteret W(s, t) (Figur 3) er estimert ved å beregne autokorrelasjonen til alle wavelets i wavelet spekteret W(s, t). De beregnede autokorrelasjonene, WA(R(s), m), for wavelet-spektret, W s, t), har maksimale korrelasjoner (R) i følgende perioder: WA(R(maks), Tdco2()) = [(0.5, 3), (0.5, 9), (0.4, 18), (0.42, 33)] (Figur 4). De identifiserte stasjonære dCO2 perioden, har korrelasjoner R()=[0.5, 0.5, 0.4, 0.4] til periodene: Tdco2() = [3, 9, 33, 64] (år.).

CO2 og signaturen havets overflatetemperatur

Lunar nodal drevet temperaturperioder i havet, har stasjonære perioder på Tln() = [1/3, 1, 4, 7]18.61/2 =[3.1, 9.3, 37.2, 65.1] år. Feilavviket [Tln()-Tdco2] = [0, 0, 4, 1] år, som har et midlere avvik på bare 1.25 år.

Veksten i bakgrunn nivået for CO2, dCO2, har altså signaturen til Lunar Nodal Tide. Lunar Nodal Tide er en stående tidevannsbølge mellom pol og ekvator, styrt av en slingring på 18.6 år i jordaksen (Earth nutation), styrt av månen. Denne er beskrevet på en rekke poster, her på denne bloggen. Lunar Nodal Tide gir en vertikal omrøring i havet mellom kaldt bunnvann og varmet overflatevann, som gir periodiske temperatur-endringer i havets overflate på n*18.6 år. CO2-vekst har altså signaturen til Lunar Nodal Tide, styrt av Månen. Det tyder på at veksten i bakgrunns-nivået for CO2, er temperaturendringer i havets overflate, drevet av et Lunar Nodal Temperatur spektrum.

Denne CO2 data serien dekker en tidsperiode på ca. 60 år. Det betyr at en kan forvente at periodiske endringer i lengre CO2 dataserier kan forklares med lengre perioder i Lunar Nodal Spektrum.

Kilden til lunar nodal spektrum er altså tidevannet, Lunar nodal tide, som påvirkes av en periodisk endring i jordaksen på 18.6 år (Nutasjonen), som påvirkes av gravitasjonen mellom Jorden, Solen og Månen. Rekkevidden av dette er at det er at veksten i bakgrunns-nivået for CO2, har Lunar-drevet forutsigbare endringer. 

Akkumulert CO2 og global havoverflate temperatur

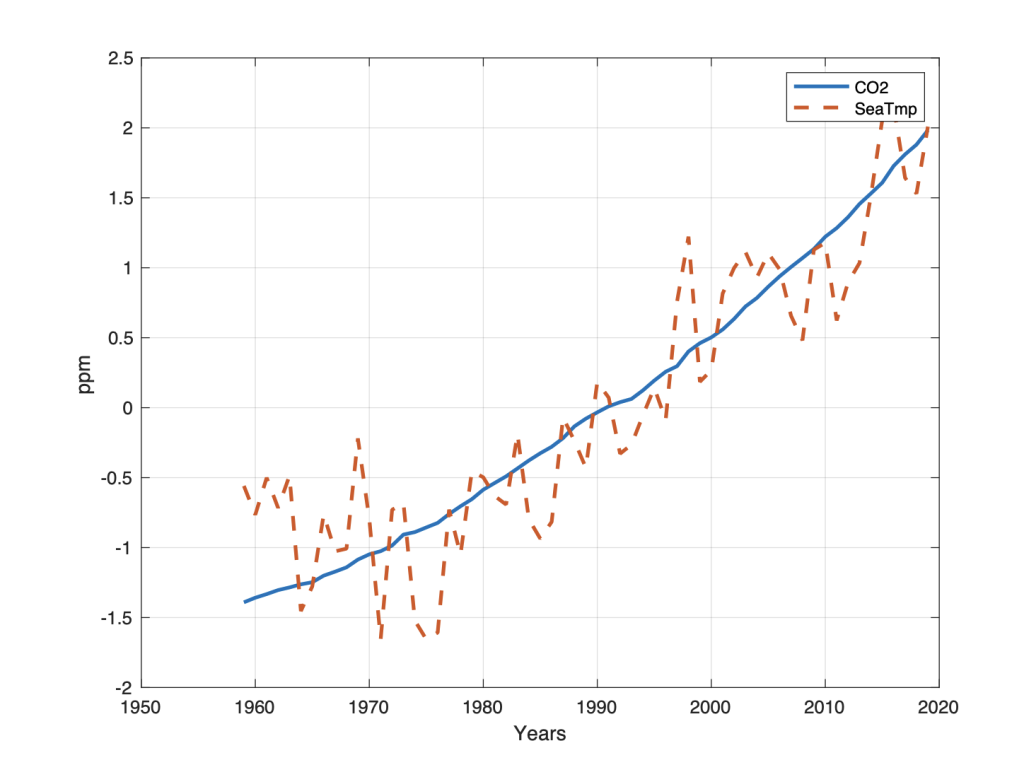
Figur 6. Skalert måling av CO2 (Mauna Loa) og skalert Global havoverflate temperatur (SeaTemp) (HadSST3) for perioden 1959 til 2020.

Figur 6 viser utvikling av CO2 (Mauna Loa) og global havoverflate temperatur (HadSST3) for perioden 1959 til 2020. Begge dataseriene er skalert etter (y(t() = (x(t)-E[x(t)])/var[x(t)]). Det framgår av Figur 5 en direkte sammenheng mellom CO2 og global havtemperatur (SeaTem) i perioden 1980-2020. Krysskorrelasjonen mellom CO2 og SeaTem er beregnet til R=0.9. 

Global havtemperaturer og CO2 har perioder på 9 år, der CO2 har en tidsforsinkelse på ca. 2.0 år. Det tilsvarer en fase-forsinkelse på ca pi/2. Det betyr at bakgrunnsnivået for CO2 reduseres, går i negativ retning, (+0), når havtemperaturen W2gst(s=9,t), veder fra et maksimum, og går i negativ retning (mot lavere temperatur. Det betyr hastigheten i utfelling av CO2 har et maksimum, når havtemperaturen har et maksimum.

Kommentar

Når CO2 (Mauna Loa) og Global havtemperatur har samme signatur (frekvensspekter), er det en bekreftelse på at de har samme kilde som forårsaker variasjonene.

Det denne enkle undersøkelsen viser, er at veksten i CO2 (Mauna Loa) fra 1958-2020, har en Lunar-drevet signatur. Lunar drevet signatur har sin første årsak fra en endring i jordrotasjonen på 18.6 år, styrt av månen. Denne perioden fører til en stående tidevannsbølge på 18.6 år mellom pol og ekvator. Tidevann bølgen på 18.6 år fører tid drevet vertikal miksing, mellom kaldt bunnvann og varmt overflatevann, med en periode på [18.6/2, 18.6, 2*18.6, 3*18.6,,,]år. En Lunar-drevet signatur i CO2-vekst tyder altså på at det er global oppvarming av havet, som er den primære kilden til CO2-vekst i atmosfæren, og ikke omvendt. Det er altså Månen som er synderen, i striden om global oppvarming. Som vi skal se etter hvert, Månen har Solen som hjelper i over lengre perioder.

På Figur 5 ser vi at CO2 fortsetter å vokse etter at global oppvarming har stabilisert seg etter år 2006. Forklaringen er at global oppvarming bestemmer hastigheten i CO2 vekst. Veksten i CO2 er størst ved maksimal temperatur. Det betyr at bakgrunns-nivået for CO2, vil forsette å vokse, inntil den globale oppvarming snur, og vi går inn i en kaldere klimaperiode.

Referanser

1 The Mauna Loa, C02 data series 1958-2020 The Mauna Loa, Hawaii CO2 data series cover the period 1958-2020, which is the longest continuous record of direct atmospheric CO2 measurements. Data are recorded at an altitude of 3400 m in the northern subtropics, which is not the same as the globally averaged CO2 concentration at the surface. The data series is managed by NOAA Global Monitoring Laboratory. https://gml.noaa.gov/ccgg/trends/data.html.

2. The Earth’s global mean temperature is represented in this investigation by the HadCRUT4 data series, covering the period from 1850 to 2020. These data series are based on sea surface and land-air temperature estimates (Morice et al. 2012). The sea surface temperature data series (HadSST3) consists of anomalies on a 5°-by-5° global grid, while the land-air temperature data series (CRUTEM4) consists of anomalies on a 5°-by-5° grid and is supported by the Climatic Research Unit (http://www.metoffice.gov.uk/hadobs/hadcrut4/).

3. Climate Clock: Lunar Forced Global varming: